Welcome to the first in a series of articles focusing on electrical calculation basics. This month, we'll discuss the most fundamental of calculations — those for current (I) and kilowatts (kW). We'll also show you how you can do these calculations “in your head,” with very reasonable accuracy, through the use of constants.
You may ask, “What exactly is a constant?” An example of a constant with which you're very much familiar is pi (π), which is derived by dividing a circle's circumference by its diameter. No matter what the circumference and diameter of the respective circle, their ratio is always pi. You can use constants that apply to specific single- and 3-phase voltages to calculate current (I) and kilowatts (kW). Let's see how to do this.
Single-Phase Calculations
Basic electrical theory tells us that for a single-phase system,
kW = (V × I × PF) ÷ 1,000.
For the sake of simplicity, let's assume the power factor (PF) is unity. Therefore, the above equation becomes
kW = (V × I) ÷ 1,000.
Solving for I, the equation becomes
I = 1,000kW ÷ V (Equation 1)
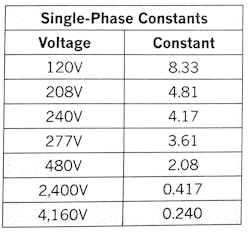
Now, if we look at the “1,000 ÷ V” portion of this equation, you can see that by inserting the respective single-phase voltage for “V” and dividing it into the “1,000,” you get a specific number (or constant) you can use to multiply “kW” to get the current draw of that load at the respective voltage.
For example, the constant for the 120V calculation is 8.33 (1,000 ÷ 120). Using this constant, Equation 1 becomes
I = 8.33kW.
So, if you have a 10kW load, you can calculate the current draw to be 83.3A (10 × 8.33). If you have a piece of equipment that draws 80A, then you can calculate the relative size of the required power source, which is 10kW (80 ÷ 8.33).
By using this same procedure but inserting the respective single-phase voltage, you get the following single-phase constants, as shown in Table 1.
3-Phase Calculations
For 3-phase systems, we use the following equation:
kW = (V × I × PF × 1.732) ÷ 1,000.
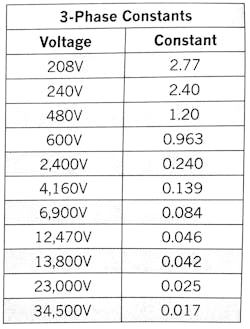
Again, assuming unity PF and solving this equation for “I,” you get:
I = 1,000kW ÷ 1.732V.
Now, if you look at the “1,000 ÷ 1.732V” portion of this equation, you can see that by inserting the respective 3-phase voltage for “V” and multiplying it by 1.732, you can then divide that resulting quantity into “1,000” to get a specific number (or constant) you can use to multiply “kW” to get the current draw of that 3-phase load at the respective 3-phase voltage. Table 2 lists each 3-phase constant for the respective 3-phase voltage obtained from the above calculation.