Suppose a plant has a high rate of electronics failures, daily loss of at least one motor bearing, and complaints of tingling or shock when people touch water fountains or production equipment. These problems have one thing in common: current is flowing where it isn’t supposed to flow. Common wisdom would point toward grounding problems, so would you solve this by driving ground rods at the trouble spots?
Driving ground rods won’t solve the problem because it doesn’t put metallic objects at equipotential. How do we know this? Again, we apply Ohm’s Law. A bonding jumper has such low resistance that you can consider it to be zero; voltage is current times resistance so it ends up being zero. But soil has much higher resistance, and that resistance varies. Driving ground rods does not produce equipotential due to the resistance that’s still there.
Many “solutions” to problems resulting from bonding deficiencies are expensive yet ineffective. But a length of wire and two connectors costs very little and will “amazingly” bring undesired current flow to zero.
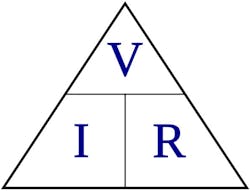
This is just one example of applying one item from basic electrical theory. How much of that basic theory have you forgotten? If someone asked you the formula for calculating voltage if resistance and current are known, do you have to look it up? It’s not a bad idea to take the time to periodically review basic theory.
Let’s reinforce that point by expanding on this example. Suppose the plant engineer decides that driving ground rods at the trouble spots is the correct solution. You ask why, and he says, “Because electricity takes the path of least resistance. Everyone knows that.”
Now, you could draw out the bonding circuits and walk him through the Ohm’s Law calculations. But he’s got this false idea in his head. You need to tackle that first. To do that, turn to Kirchoff’s Law of Parallel Circuits.
This law states that electricity flows in inverse proportion to the resistances before it. If your circuit has two 100 ohm resistors in parallel, half the current will flow through each one. Let’s say that because of small differences in manufacturing tolerances, it turns out they differ by 0.0001 ohms. According to the plant engineer’s theory, current will flow through only one of these resistors. From your basic electrical theory, you know the “least path of resistance” idea is flatly wrong.
Now keep in mind that electricity always tries to get back to the source; this is what makes the current flow in a “circuit” (think “circle”) rather than in some other arrangement. It goes out from the source, and flows back through the available paths to the source.
Suppose the path from a particular trouble spot (e.g., a motor casing) through the soil and back to the source is 20,000 ohms. And suppose the path through the motor bearings back to the source is 100 ohms. Is that ground rod really doing anything? If you’re unsure, draw this circuit and calculate the current flowing through each path assuming a 480V supply. Better get some strawberry jam for those bearings, because they are toast.
About the Author

Mark Lamendola
Mark is an expert in maintenance management, having racked up an impressive track record during his time working in the field. He also has extensive knowledge of, and practical expertise with, the National Electrical Code (NEC). Through his consulting business, he provides articles and training materials on electrical topics, specializing in making difficult subjects easy to understand and focusing on the practical aspects of electrical work.
Prior to starting his own business, Mark served as the Technical Editor on EC&M for six years, worked three years in nuclear maintenance, six years as a contract project engineer/project manager, three years as a systems engineer, and three years in plant maintenance management.
Mark earned an AAS degree from Rock Valley College, a BSEET from Columbia Pacific University, and an MBA from Lake Erie College. He’s also completed several related certifications over the years and even was formerly licensed as a Master Electrician. He is a Senior Member of the IEEE and past Chairman of the Kansas City Chapters of both the IEEE and the IEEE Computer Society. Mark also served as the program director for, a board member of, and webmaster of, the Midwest Chapter of the 7x24 Exchange. He has also held memberships with the following organizations: NETA, NFPA, International Association of Webmasters, and Institute of Certified Professional Managers.