Last month's Code Calculations article covered transformer calculation definitions and some specifics of delta transformer calculations. This month we turn our attention to the differences between delta and wye transformers and to wye transformer calculations. We'll close by looking at why it's so important to know how to perform these calculations, but you'll likely see the reasons as we go.
In a wye configuration, three single-phase transformers are connected to a common point (neutral) via a lead from their secondaries. The other lead from each of the single-phase transformers is connected to the line conductors. This configuration is called a “wye,” because in an electrical drawing it looks like the letter Y. Unlike the delta transformer, it doesn't have a high leg.
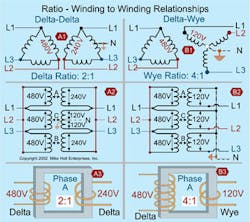
Differences in wye and delta transformers. The ratio of a transformer is the relationship between the number of primary winding turns to the number of secondary winding turns — and thus a comparison between the primary phase voltage and the secondary phase voltage. For typical delta/delta systems, the ratio is 2:1 — but for typical delta/wye systems, the ratio is 4:1 (Fig. 1 above).
If the primary phase voltage in a typical delta/delta system is 480V, the secondary phase voltage is 240V. If the primary phase voltage in a typical delta/wye system is 480V, the secondary phase voltage is 120V.
Delta and wye transformers also differ with regard to their phase voltage versus line voltage and phase current versus line current. In a delta transformer,
EPhase=ELine and ILine=IPhase×√3.
In a wye transformer,
IPhase=ILine and ELine=EPhase×√3.
These differences affect more than just which formulas you use for transformer calculations. By combining delta/delta and delta/wye transformers, you can abate harmonic distortion in an electrical system. We'll look at that strategy in more detail after addressing wye transformer calculations.
Wye current and voltage calculations. In a wye transformer, the 3-phase and single-phase 120V line current equals the phase current (IPhase = ILine) (Fig. 2 on page C20).
Let's apply this to an actual problem. What's the secondary phase current for a 150kVA, 480V to 208Y/120V, 3-phase transformer (Fig. 3 on page C20)? ILine=150,000VA÷(208V×1.732)=416A, or IPhase=50,000VA÷120=416A
To find wye 3-phase line and phase voltages, use the following formulas:
EPhase=ELine÷√3
ELine=EPhase×√3
Since each line conductor from a wye transformer is connected to a different transformer winding (phase), the effects of 3-phase loading on the line are the same as on the phase (Fig. 4 on page C21). A 36kVA, 208V, 3-phase load has the following effect:
Line power=36kVA
ILine=VALine÷(ELine×√3)
ILine=36,000VA÷(208V×√3)=100A
Phase power=12kVA (any winding)
IPhase=VAPhase÷EPhase
IPhase=12,000VA÷120V=100A
Wye transformer balancing and sizing. Before you can properly size a delta/wye transformer, you must make sure that the secondary transformer phases (windings) or the line conductors are balanced. Note that balancing the panel (line conductors) is identical to balancing the transformer for wye transformers. Once you balance the wye transformer, you can size it according to the load on each phase. The following steps will help you balance the transformer:
Step 1: Determine the loads' VA ratings.
Step 2: Put one-third of the 3-phase load on Phase A, one-third on Phase B, and one-third on Phase C.
Step 3: Put one-half of the single-phase, 208V load on Phase A and Phase B, or Phase B and Phase C, or Phase A and Phase C.
Step 4: Place 120V loads (largest to smallest): 100% on any phase.
Now consider the following wye transformer sizing example: What size transformer (480V to 208Y/120V, 3-phase) would you need for the following loads: 208V, 36kVA, 3-phase heat strip; two 208V, 10kVA, single-phase loads; and three 120V, 3kVA single-phase loads?
a) three single-phase, 25kVA transformers
b) one 3-phase, 75kVA transformer
c) a or b
d) none of these
Phase A=23kVA
Phase B=22kVA
Phase C=20kVA
The Table sums up the kVA for each phase of each load. Note that the phase totals (23kVA, 22kVA, and 20kVA) should add up to the line total (65kVA). Always use a “checksum” like this to ensure you have accounted for all items and the math is right.
If you're dealing with high-harmonic loads, the maximum unbalanced load can be higher than the nameplate kVA would indicate. Matching the transformer to the anticipated load then requires a high degree of accuracy if you want to get a reasonable level of either efficiency or power quality.
One approach to such a situation is to supply high-harmonic loads from their own delta/delta transformer. Another is to supply them from their own delta/wye and double the neutral. The approach you choose will depend on the characteristics of your loads and how well you lay out your power distribution system.
For example, you might put your computer loads (which have switching power supplies) on a delta/delta transformer, which you would feed from a delta/wye transformer. This would greatly reduce the presence of harmonics in the primary system, partly due to the absence of a neutral connection. But the behavior of the delta/delta transformer itself, combined with the interaction of delta/delta and delta/wye, will also cause a reduction in harmonics. Notice the word “might” in the question of whether to implement this kind of design. Grounding considerations can make it an undesirable approach, depending on the various loads and the design of the overall electrical system. Keep in mind that this is one of the many ways to mix and match transformers to solve power quality problems.
Due to uptime or power quality concerns with complex loads, you may need to mix and match transformer configurations as in the previous example. And that's something you can't do unless you understand both delta and wye calculations.
Another issue is proper transformer loading. As a rule of thumb, 80% loading is a good target. If you overload the transformer, though, it goes into core saturation and output consists of distorted waveforms. The clipped peaks typical of saturated transformers cause excess heating in the loads. This issue of transformer loading means you're going to have to perform the transformer calculations just to get basic power quality and reasonable efficiency.
So it's important not to oversimplify your approach to transformer selection. It's usually best to do all the calculations using the nameplate kVA. Then, design the distribution system as though all loads are linear. When that's done, identify which loads are high harmonic, such as electronic ballasts, computer power supplies, and motors with varying loads. At this point, you can efficiently work with a transformer supplier to develop a good solution.
Now that you understand delta and wye transformer calculations, you can see how important they are to being able to do a quality installation any time you're specifying transformers or considering adding loads to existing transformers. This ability is also important if you're trying to solve a power quality problem or a problem with “unexplained” system trips. You may wish to sharpen this ability by purchasing an electrical calculations workbook or taking on this kind of work in your electrical projects.
