Taking the Mystery Out of Sizing Pull Boxes and Junction Boxes

Courtesy of www.MikeHolt.com. Based on the 2020 NEC.

Pull boxes, junction boxes, and conduit bodies must be sized to allow conductors 4 AWG and larger to be installed without damage to the conductor insulation. The NEC provides sizing requirements in Sec. 314.28.

Keep in mind these requirements address conductors used for general wiring, such as those identified in Table 310.16. The requirements do not apply to other types of wiring or cabling. A specialty signal cable might have a bend radius of 24 in. and that would require a significantly larger pull box than what you’d use for a general wiring conductor of a similar-sized outer jacket.

Minimum dimensions

For straight pulls when raceways contain conductors 4 AWG or larger, the minimum distance from where the raceway containing conductors enter to the opposite wall must be at least eight times the trade size of the largest raceway. A straight-pull calculation applies when raceways containing conductors enter one side of a box and leave through the opposite wall of the box [Sec. 314.28(A)(1)].

For other types of pulls where the raceways contain conductors 4 AWG or larger, these rules apply [Sec. 314.28(A)(2)]:

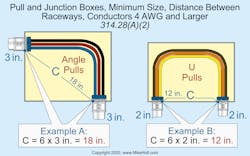
Angle pulls. These occur when raceways containing conductors enter a wall and leave through one that’s 90º from the entry wall. The distance from the raceway entry to the opposite wall must be at least six times the trade size of the largest raceway, plus the sum of the trade sizes of the remaining raceways on the same wall and row.
U pulls. A raceway containing conductors that enters and leaves from the same wall is a U pull. The distance from where the raceways enter to the opposite wall must be at least six times the trade size of the largest raceway, plus the sum of the trade sizes of the remaining raceways on the same wall and row.
Splices. When conductors are spliced, the distance from where the raceways enter to the opposite wall must be at least six times the trade size of the largest raceway, plus the sum of the trade sizes of the remaining raceways on the same wall and row.
Rows. Where there’s more than one row of raceway entries on the same wall, each row is calculated individually, and the row with the largest distance must be used.
Distance between raceway entries. The distance between raceway entries enclosing the same conductor must be at least six times the trade size of the largest raceway, measured from the raceways’ opening nearest edge to the nearest edge (Fig. 1).

Fig. 1. The distance between raceway entries enclosing the same conductor must be at least six times the trade size of the largest raceway. — **Fig. 1.** The distance between raceway entries enclosing the same conductor must be at least six times the trade size of the largest raceway.

The measurement between raceway entries is taken from the actual raceway entry, not the locknuts or bushings used to terminate the raceways.

When conductors enter an enclosure with a removable cover, such as a conduit body or wireway, the distance from where the conductors enter to the removable cover must be at least the bending distance listed in Table 312.6(A) for one conductor per terminal [Sec. 314.28(A)(2) Exception].

Pull box example 1

A junction box contains four trade size 3 raceways: two on the left side, one on the right side, and one on the bottom. The conductors from one of the trade size 3 raceways on the left wall are pulled through the trade size 3 raceway on the right wall. The conductors from the other trade size 3 raceway on the left wall are pulled through a trade size 3 raceway at the bottom of the pull box.

What’s the horizontal dimension of this box (Fig. 2)?

Fig. 2. As noted in this example, the minimum horizontal distance of the box is 24 in. — **Fig. 2.** As noted in this example, the minimum horizontal distance of the box is 24 in.

Solution: Left to right straight pull = 8 × 3 in. = 24 in. Right to left straight pull = 8 × 3 in. = 24 in. Left to right angle pull = (6 × 3 in.) + 3 in. = 21 in. Right to left angle pull = no calculation

Answer: 24 in. [Sec. 314.28]

What’s the vertical dimension of this box?

Solution: Top to bottom straight pull = no calculation.

Bottom to top straight pull = no calculation.

Top to bottom angle pull = no calculation.

Bottom to top angle pull = 6 × 3 in. = 18 in.

Answer: (a) 18 in. [Sec. 314.28]

What’s the minimum distance between the two trade size 3 raceways containing the same conductors?

Solution: 6 × 3 in. = 18 in.

Answer: (a) 18 in. [Sec. 314.28]

Pull box example 2

A pull box contains a trade size 2 and trade size 3 raceway on the left side, a trade size 3 raceway on the top, and a trade size 2 raceway on the right side. The trade size 2 raceways are a straight pull, and the trade size 3 raceways are an angle pull.

What’s the horizontal dimension of this box?

Solution: Left to right straight pull = 8 × 2 in. = 16 in.

Right to left straight pull = 8 × 2 in. = 16 in.

Left to right angle pull = (6 × 3 in.) + 2 in. = 20 in.

Right to left angle pull = no calculation.

Answer: (a) 20 in. [Sec. 314.28(A)(2)]

What’s the vertical dimension of this box (Fig. 3)?

Fig. 3. As noted in this example, the minimum vertical distance of the box is 18 in. — **Fig. 3.** As noted in this example, the minimum vertical distance of the box is 18 in.

Solution: Top to bottom straight pull = no calculation.

Bottom to top straight pull = no calculation.

Top to bottom angle pull = 6 × 3 in. = 18 in.

Bottom to top angle pull = no calculation.

Answer: (b) 18 in. [Sec. 314.28(A)(2)]

If the two trade size 3 raceways contain the same conductors, what’s the minimum distance between these raceways?

Solution: 6 × 3 in. = 18 in.

Answer: (a) 18 in. [Sec. 314.28(A)(2)]

SIDEBAR

Quick Tips for Pull Box Sizing

Tips for learning:

Pull box calculations become easier with more practice. Use practical field examples to practice calculations.
Draw up some sample pull boxes and calculate them.
Obtain drawings from a completed project and “reverse engineer” the box sizes by calculating them.

Tips for doing:

Draw out the problem.
To avoid simple mistakes, take your time, and be methodical.
Do one wall at a time, and remember which wall you’re working on.
Calculate the horizontal distance(s):

Left to right straight calculation
Right to left straight calculation
Left to right angle or U pull calculation
Right to left angle or U pull calculation

Calculate the vertical distance(s):

Top to bottom straight calculation
Bottom to top straight calculation
Top to bottom angle or U pull calculation
Bottom to top angle or U pull calculation

Calculate the distance between raceways enclosing the same conductors.

These materials are provided to us by Mike Holt Enterprises in Leesburg, Fla. To view Code training materials offered by this company, visit www.mikeholt.com/code.